Công thức tính hình tròn diện tích & chu vi đã được học thời còn ngồi trên ghế nhà trường. Nhưng đã lâu, chúng ta không sử dụng đến nên khó tránh khỏ quên và nhầm lẫn. Vì vậy hôm nay Antoanyte.vn sẽ hướng dẫn lại một cách đơn giản và dễ hiểu nhất.
Thế nào là hình tròn?
Đường tròn là tập hợp của những điểm nằm trên cùng một mặt phẳng. Giữa hai điểm cố định được cách nhau một khoảng gọi là bán kính. Những điểm cho trước được gọi là tâm đường tròn.

Hay nói cách khác đường tròn chính là độ dài của đoạn thẳng, được giới hạn bởi ba điểm thẳng hàng. Trong đó là hai điểm không cố định và một điểm cố định là tâm đường tròn. Có nghĩa rằng, đường kính sẽ có chiều dài gấp đôi so với bán kính.
Hình tròn là phần mặt phẳng đã được giới hạn bởi đường tròn. Và chúng ta có thể đo được độ dài của từng mặt phẳng một cách dễ dàng bằng cách dùng thước đo độ dài.
Công thức tính chu vi hình tròn
Khái niệm
Chu vi hình tròn hay còn gọi là độ dài đường tròn, đây là đường biên giới hạn ngăn cách giữa bên trong với bên ngoài hình tròn.
Công thức
Chu vi hình tròn được tính theo công thức: Đường kính nhân với số Pi hoặc hai lần bán kính nhân với số Pi.
Công thức tính chu vi hình tròn chính là bằng 2 lần bán kính nhân với Pi.
C = r x 2 x 3.14.
Tính chu vi hình tròn theo đường kính bằng chính đường kính nhân với Pi.
C = d x 3.14.
Trong đó:
+ r: Bán kính hình tròn
+ d: Đường kính hình tròn
+ π: Hằng số Pi (π=3.14)
Để tính diện tích hình tròn hoặc chu vi hình tròn là phải xác định đường kính của nó. Đường kính là chiều dài của một đường bắt đầu từ cạnh của vòng tròn, đi qua tâm của vòng tròn và kết thúc ở cạnh đối diện của vòng tròn. Để đo, bạn sẽ cần một thước thẳng đo từ 1 điểm nằm trên vòng tròn và đi qua tâm tới điểm đổi diện.
Khi bạn có đường kính (d) của hình tròn, bạn có thể tìm bán kính (r) bằng công thức d = 2 x r. Bán kính của hình tròn là khoảng cách từ tâm của hình tròn đến bất kỳ điểm nào trên cạnh của hình tròn. Bán kính cũng bằng một nửa đường kính. Nếu đường kính của bạn là một số đơn giản, bạn có thể tính bán kính trong đầu. Nếu không, sắp xếp lại công thức để tìm r (r = d/2) và giải.
Ý nghĩa
Bởi vì đường tròn không thể dùng thước để đo nên bạn có thể sử dụng cách tính chu vi hình tròn để biết được chiều dài của đường tròn.
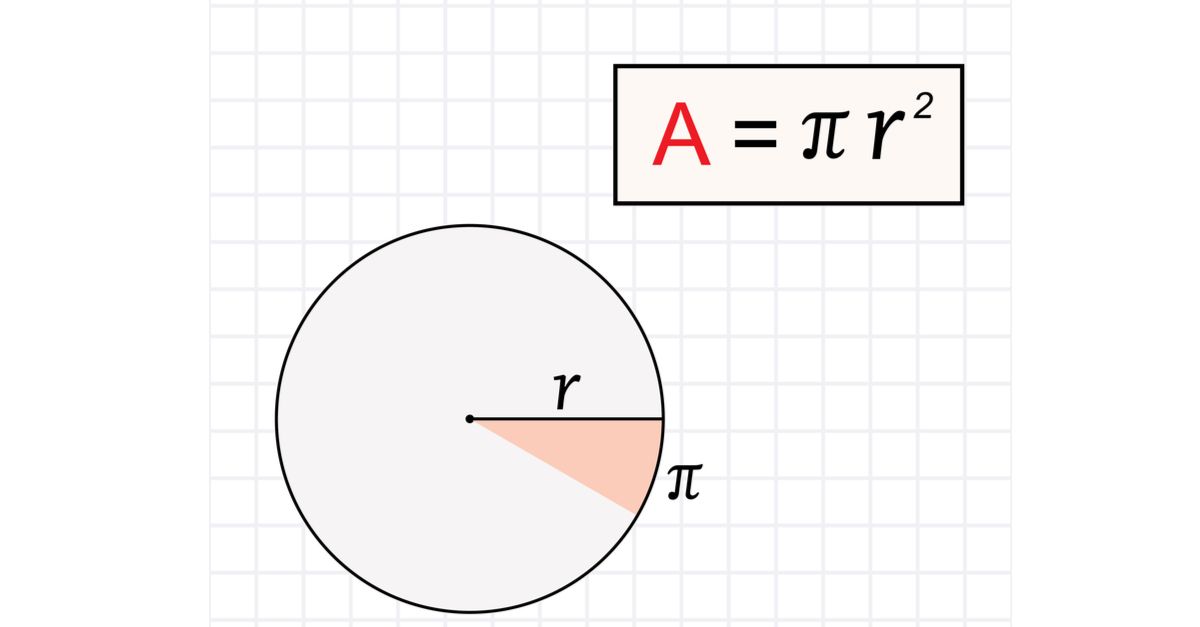
Công thức tính diện tích hình tròn
Khái niệm
Tính diện tích hình tròn là tính diện tích phần nằm bên trong đường tròn.
Công thức
Diện tích của hình tròn được tính theo công thức sau đây: S = Pi X R2
Trong đó:
- S là kí hiệu của diện tích hình tròn
- R là ký hiệu của bán kính đường tròn (R có giá trị bằng 1/2 của đường kính)
- Pi có giá trị xấp xỉ bằng 3,141, là hằng số cố định
Ví dụ minh họa 1: Giả sử hình tròn C có đường kính là 10 cm. Tính diện tích hình tròn C.
Trả lời: Áp dụng công thức tính diện tích hình tròn ta có: S = Pi X R2 = 3.14 x 102 = 3.14 x 100 = 314 cm2
Vậy diện tích hình tròn là 314 cm2.
Chu vi của hình tròn có công thức C = d.Pi = 2r.Pi. Suy ra bán kính của hình tròn là r = C/(2Pi). từ đó ta có công thức tính diện tích hình tròn là S=C2/(4Pi).
Ví dụ minh họa 2: Biết chu vi của hình tròn là 15,33 cm. Vậy diện tích hình tròn được tính như thế nào?
Trả lời:
Chu vi của hình tròn là C = d.Pi = 2r.Pi => bán kính của hình tròn là r = C/(2Pi)
Áp dụng công thức tính diện tích hình tròn S = Pi.r2. Suy ra S = Pi. (C/2Pi)2 = 18,71 cm2. Vậy diện tích hình tròn bằng 18,71 cm2.
Dựa vào đường kính hình tròn
Khi biết đường kính, ta tính được công thức diện tích hình tròn như sau: S = Pi x (d/2)2.
Trong đó: S là diện tích, d là đường kính.
Ví dụ minh họa: Đường kính hình tròn C là 8cm. Hãy tính diện tích hình tròn.
Trả lời: Áp dụng công thức ta có: S = 3.14 x (8/2)2 = 50.265 cm2.
Dựa vào hình quạt
Ta có: S = Shq x ( 360/C)
Trong đó S là diện tích hình tròn toàn phần, Shq là diện tích hình quạt, C là số đo ở góc tâm.
Ý nghĩa
Công thức tính diện tích hình tròn giúp bạn tính được toàn bộ diện tích bề mặt nằm bên trong vòng tròn.
Cách tính diện tích hình quạt tròn
Khái niệm
Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và một cung tròn chắn bởi hai bán kính này.
Công thức
Diện tích hình quạt tròn được tính theo công thức:
Trong đó:
+ r: Bán kính hình tròn
+ π: Hằng số Pi (π=3.14)
+ l: Độ dài cung tròn
Ý nghĩa
Công thức tính diện tích hình quạt tròn giúp bạn dễ dàng tính được diện tích một phần mặt phẳng nằm bên trong vòng tròn.
Bí quyết tính nhanh diện tích của hình tròn
Hiểu rõ ý nghĩa của công thức
Các bạn cần nắm vững các khái niệm liên quan đến hình tròn như bán kính đường tròn, đường kính hình tròn, tâm đường tròn. Từ đó sẽ hiểu rõ bản chất của công thức là gì? Tại sao lại có công thức này, Điều này sẽ giúp các bạn ghi nhớ được lâu hơn công thức.
Khi đã ghi nhớ công thức thì bắt tay vào ngay để làm các bài tập. Quá trình thực hành sẽ giúp các bạn sử dụng công thức một cách nhuần nhuyễn hơn.
Công thức tính diện tích hình tròn liên quan đến hằng số Pi. Vì vậy cần phải nhớ giá trị của Pi là 3,14.
Liên hệ công thức với thơ ca
Công thức về hình học luôn khô khan, khó nhớ, khó thuộc. Do vậy các bạn có thể biến công thức thành một bài thơ dí dỏm để học thuộc.
Đây là bài thơ về công thức tính diện tích hình tròn:
“Hình tròn diện tích giản đơn
Bình phương bán kính ta nhân ngay vào
Ba phảy mười bốn phía sau
Chu vi cũng dễ tính mau bạn à
Đường kính ta lấy nhân ra
Ba phảy mười bốn, thế là đã xong”.
Với bài thơ này các bạn có thể học mọi lúc, mọi nơi, rất dễ nhớ và thuộc lòng.
Giải toán bằng thơ
Việc giải toán bằng thơ sẽ giúp các em học sinh cảm thấy thích thú hơn và ham học hơn, tò mò hơn. Làm cho các giờ học trở nên sinh động hơn, vui nhộn hơn.
Các bạn có thể sưu tầm để tạo nên bí quyết học cho riêng mình nhé.
Luyện bài tập thường xuyên hơn
Toán học có rất nhiều công thức khác nhau, mỗi công thức lại có nhiều định lượng khác nhau. Do vậy để có thể nhớ được lâu hơn thì các bạn cần sử dụng công thức thường xuyên hơn. Nếu bỏ qua chúng một thời gian dài không sử dụng đến thì chúng ta rất dễ quên.
Để giúp các bạn có thể ghi nhớ lâu công thức tính diện tích & chu vi hình tròn. Hãy thường xuyên làm bài tập về hình học có liên quan đến công thức nhé. Các công thức thường có mối liên hệ đến nhau. Do đó chỉ cần bỏ sót một công thức nào là không thể chinh phục được các bài tập. Chúc các bạn thành công với bộ môn toán hình học nhé.




